Недетские игры с большими и бесконечными данными и криптотехнологиями
В мировой практике набирают обороты массовые внедрения нейронных сетей, тензорных вычислений и других направлений развития искусственного интеллекта. В данных исследованиях мы попробуем раскрыть другую сторону развития этого направления — применение систем искусственного интеллекта в анализе больших и бесконечных данных и определим способы управления ошибкой обучения нейросетей. Мы попробуем заставить математическую базу, статистику и возможности систем искусственного интеллекта сформировать нам преимущество перед любой сколь угодно сложной системой. Задачу математическому аппарату, статистике и искусственному интеллекту мы поставим самую жесткую, которую обычному неподготовленному участнику соревнований решить не представляется возможным.
Условия проведения испытаний
Алгоритм шифрования и исходные условия состязания:
- Соревнуются два участника, загадывая две строки с каждой стороны [SERVER SEED], [CLIENT SEED].
- Каждая итерация соревнования нумеруется ее порядковым номером [NONCE], это значение будет также участвовать в состязании в качестве «соли безопасности» в обоих сторонах.
- В ходе соревнований формируются две строки для определения результатов состязания:
- STRING1 = «[NONCE]: [SERVER SEED]: [NONCE]»
- STRING2 = «[NONCE]: [CLIENT SEED]: [NONCE]»
- Затем HMAC-SHA512 используется для хэширования STRING1 с STRING2 в качестве секретного ключа, давая нам шестнадцатеричную строку из 128 символов.
- Первые 8 символов полученной шестнадцатеричной строки берутся и преобразуются в десятичную, остальные значения — отбрасываются.
- Затем это значение, преобразованное в десятичную дробь делится на 429496,7295 и округляется до ближайшего целого числа.
- Полученное целое число используется в качестве значения определения результатов состязаний, с минимально возможным значением 1 и максимально возможным значением, равным 10000.
- Для проверки, что сервис со стороны Сервера не жульничает, загаданная строка [SEED SERVER] хэшируется алгоритмом SHA256 и значение функции SHA256([SEED SERVER]) заранее известно стороне — Клиенту, которую он может свободно проверить для каждой итерации, например здесь.
Оценка условий соревнований
На первый взгляд условия для обоих сторон — прозрачные и ставят обе стороны в равные состязательные условия: два участника просто загадали случайные строки. Результат соревнования на первый взгляд кажется непредсказуемым для каждой из сторон — никто не знает, какую последовательность каждая из сторон загадала. Результат состязаний заведомо подчиняется нормальному закону распределения, и статистический успех каждой из сторон в состязании соответственно равен 0,5, или 50%. Но в условиях состязаний есть одно но, которое должно насторожить: стороне-Клиенту заранее известно значение функции SHA256([SEED SERVER]), хоть для предопределения результата состязания оно кажется непригодным в силу:
- Сложности результата применения последовательностей шифрования (SHA256/HMAC-SHA512). Заранее уведомим, что даже один алгоритм реализации контрольной суммы SHA256 реализует последовательное применение шести жесточайших функций, обезличивающих исходные данные.
- Привнесения в состязания стороннего параметра [NONCE].
- Случайных удалений полных результатов шифрования ключом HMAC-SHA512 до 8 символов.
- Проведения арифметических операций.
Что будет в случае если Клиент применит математический аппарат и возможности искусственного интеллекта для формирования преимущества в свою сторону?
На первый взгляд условия максимально жесткие и решить задачу формирования преимущества в сторону Клиента невозможно. Контрольная сумма SHA256 имеет криптостойкость 2512, которой достаточно, чтобы обезоружить сторону, пытающуюся предопределить исход состязаний. Но не будем сдаваться и приступим к решению задачи, коротко описав условия состязаний: присвоение приза Клиенту производится в случае угадывания Клиентом результирующего значения, описанного в «Условиях проведения испытаний» в диапазоне более или менее 5000 на выборке от 1 до 10 000 ( классический вариант «больше-меньше»).
Исходные данные, имеющиеся у стороны-Клиента:
- [SERVER SEED HASH]
- [CLIENT_SEED]
- [NONCE]
Цель состязаний Клиента — получить статическое преимущество положительной результативности в свою пользу более 0,5 исходов, или более 50%.
Подготовка к соревнованиям
1. Первый шаг к получению преимущества — имеющаяся возможность проверки корректности результатов состязаний, расположенная тут. Параметры, передаваемые для проверки значений, наглядно представлены в примере «Условия проведения испытаний».
Имеющийся у Клиента параметр [SERVER_SEED_HASH] в силу самой технологии получения контрольной суммы имеет статическую длину — 64 байта, или 512 бит. Код страницы проверки значений доступен в исходном виде, скачивается без проблем для последующих модификаций. Двери открыты — начнем модифицировать его под свои нужды. Для начала приведем доступный нам код проверки и его результаты к виду, понятному нейронным сетям (отобразим результаты формы в двоичном представлении). Исходный код наглядного представления соответственно доступен по ссылке.
В ходе модификации мы дополнили форму верификации результатов отображением значений [SERVER_SEED_HASH], [CLIENT_SEED], [NONCE] их двоичными представлениями [SERVER_SEED_HASH_B], [CLIENT_SEED_B], [NONCE_B]. В нижней части мы представили соответственно двоичный код [SERVER_SEED_HASH_B] как основного параметра обучаемой нами нейронной сети, и в результате внизу формируем соответствующее необходимое значение нейрона на выходе («1 0» — в случае, если результирующее значение более 5000, «0 1» в случае, если результирующее значение менее 5001).
2. В ходе подготовки соревнований нам понадобится обучить нейросеть принимать правильные решения. Для этого нам понадобятся большие наборы корректных данных для ее обучения. Для решения этой части задачи мы проведем вторую модификацию нашего кода страницы наглядного представления и преобразуем ее в прямой JavaScript.js код, убрав из него все лишнее, и реализуем доступность передачи в наш код Node.JS код параметров для формирования выборки обучения.
В результате мы:
- Сами сгенерируем случайный [SERVER_SEED].
- Получим его SHA256 хэш [SERVER_SEED_HASH].
- Проведем необходимые вычисления для получения результата виртуального соревнования и установления соответствия [SERVER_SEED_HASH] <->[RN], или результат состязаний.
- Таких значений получим столько, сколько нам необходимо в любой момент без необходимости тренировки в живых соревнованиях.
Небольшое отступление. Криптоскойкость алгоритма SHA256, применяемого к параметру [SERVER_SEED] => 2512. Для формирования полной выборки при прямом стандартном обучении нам не хватит места во всех дата-центрах и вычислительных мощностей, чтобы обучить нейросеть стандартно выдавать решение обратного отображения исходного [SERVER_SEED] на основе имеющейся его контрольной суммы [SERVER_SEED_HASH]. Далее мы наглядно покажем, а нужно ли нам оно вообще для получения необходимого результата и как следствие — получения статистического преимущества?! На данном этапе ограничимся земными возможностями и набором в 1 000 000 значений выборки обучения и сгенерируем столько же тестовых данных.
Чтобы не получать исходные данные для обучения и тестовые наборы через наш браузер (страницу для наглядного отображения), переделаем код страницы в удобный для нас Node.JS код, в который мы сможем передавать параметры и генерировать какие угодно наборы/выборки обучения и тестовые наборы для контроля качества обучения.
Все библиотеки Crypto-JS, использованные в эксперименте доступны по ссылке. Переделанная страница verify.html в Node.JS код для генерации данных обучения и тестовых данных— доступна для загрузки здесь.
Для обучения нейросети нам понадобится математический аппарат нейронных сетей с обратным распространением ошибки. За основу возьмем например библиотеку «Fast Artifact Neural Network», которая свободно доступна практически для всех платформ и выложена в исходных кодах и в избытке доступна в бинарных сборках. С точки зрения удобства решения задачи и экономии времени на сборку инструментария, возьмем готовое решение SFANN для платформы Linux, реализующее работу с нейросетями в командной строке.
Немного теории
Чтобы получить статистическое преимущество, Клиенту, т. е. нам, достаточно установить любым способом соответствие исходных значений соревнований результирующему значению соревнований. Несмотря на то, что у Клиента нет исходного [SERVER_SEED], у Клиента заранее есть значение функции [SERVER_SEED_HASH]=SHA256([SERVER_SEED]).
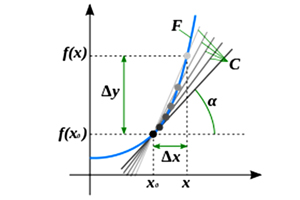
Невзирая на сложность любой функции, в качестве которой [SERVER_SEED] выступает аргументом, функция (которую должна сгенерировать наша нейросеть) будет пригодна к решению нашей задачи только в том случае, если она дифференцируема и можно получить ее первообразную. Поскольку суть хэш-функции — «однозначное определение соответствия параметру его хэш-значения», данное свойство однозначно устанавливает возможность дифференцирования функции SHA256, или возможность нахождения у нее первообразной. Это означает, что если результат соревнований определяют исходные значения: [SERVER_SEED], [CLIENT_SEED], [NONCE], то производная функция SHA256([SERVER_SEED]), а также уже известные параметры [CLIENT_SEED], [NONCE] также однозначно определяют исход состязаний.
Имеющиеся у нас функция (F1), параметризированная тремя параметрами, и неизвестная функция (F2) тождественно равны и определяют один и тот же результат:
F1([SERVER_SEED], [CLIENT_SEED], [NONCE]) <==> F2([SERVER_SEED_HASH], [CLIENT_SEED], [NONCE])
В подкрепление нашей теории приведем классическое определение производной из дифференциального исчисления: «Произво́дная функция — понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке. Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование».
Таким образом, мы установили, что для получения преимущества нам нужно найти такую функцию F2, которая предопределит результат от известных нам трех значений: [SERVER_SEED_HASH], [CLIENT_SEED], [NONCE].
В задачах классификации и нахождения форм любых функций нейронным сетям равных нет, потому используем эту возможность, заранее указав основные свойства нейронов и нейронных сетей, обучаемых на полных и неполных множествах:
- Обученный нейрон или нейронная сеть на полном обучаемом множестве значений однозначно определяет результат классификации.
- Обученный нейрон или нейронная сеть на неполном множестве значений однозначно классифицирует значение на обучаемом множестве {1..N} и в соответствии с нормальным законом распределения случайных величин, производит с бóльшей вероятностью классификацию ошибки (F2(N+1) < 0,5) на неизвестном множестве {N+1..∞} при последующих значениях N → ∞ полного множества обучения.
Предварительные выводы:
- Для того чтобы получить статистическое преимущество, в обучении нейрона на полном множестве у нас нет необходимости, а следственно нет необходимости в наличии и использовании огромных ресурсов для хранения выборки обучения, а также огромных вычислительных ресурсов для обучения нейронной сети.
- В решении задачи получения статистического преимущества нас устроит любой результат классификации значений или ошибки > 0,5, поскольку наша нейросеть на выходе имеет всего два значения. Независимо от того, какая классификация производится, принимая во внимание условия которые мы создали, нас устроит любой положительный результат: классификация самого значения (обучение на полной выборке) или классификация ошибки нахождения значения (обучение на больших выборках [Big Data] из N значений при N → ∞ ).
- При обучении на неполном множестве {1..N}, результат работы/классификации обученного нейрона также подчиняется нормальному распределению статистических величин {1..∞}.
Формируем выборки обучения и тестовые выборки
Для формирования тестовых выборок и выборок обучения, создадим несложный скрипт-код генерации данных для обучения и такой же по объему объем данных для тестирования нейрона. Заранее укажем, что в качестве [CLIENT_SEED] устанавливаем значение, равное [NONCE], чтобы не генерировать разные последовательности, которые у нас и так уже есть. Количество эпох обучения нейрона установим 10
Скрипт генерации данных обучения:
#!/bin/bash
#genldata
echo Generate $1 data for nonce $2
echo $1 512 2 > ldata.txt
for k in `eval echo {1..$1}` ; do
chars=0123456789abcdef
server_seed=""
for i in {1..64} ; do
server_seed=$server_seed${chars:RANDOM%${#chars}:1}
done
node verify.js $server_seed $2 $2 >> ldata.txt &
done
Скрипт генерации данных тестирования (аналогичен скрипту генерации данных обучения, разница только в наименовании файла, куда выводим данные):
#!/bin/bash
#gentdata
echo Generate $1 data for nonce $2
echo $1 512 2 > tdata.txt
for k in `eval echo {1..$1}` ; do
chars=0123456789abcdef
server_seed=«"
for i in {1..64} ; do
server_seed=$server_seed${chars:RANDOM%${#chars}:1}
done
node verify.js $server_seed $2 $2 >> tdata.txt &
done
Генерируем данные для обучения/тестирования (произведем генерацию 106 значений обучающих и тестовых данных, 2835 — произвольное число установит значение [NONCE]):
>./genldata.sh 100000 2835
>./genldata.sh 100000 2835
Обучаем нейронную сеть
Исполняемый модуль для обучения нейронных сетей sfann доступен для свободного скачивания из первоисточников:
Параметры обучения нашей нейросети сохраняем в скрипт trainann.sh:
#!/bin/bash
./sfann -v —do-training —train ./ldata.txt —num-hidden 2 —save-max-train ./maxtrain.ann —max-epoch 10000
#./sfann -v —do-cross-validation —train ./ldata.txt —num-hidden 2 —cv-num-folds 4 —cv-num-dev 2 —save-max-dev-run ./maxtrain.ann —max-epoch 10000
Для нашего случая соответственно количество нейронов входного слоя — 512, нейронов в скрытом слое — 2, нейронов в выходном слое — 2. В приведенном скрипте представлен пример с прямым обучением на полной выборке, а также обучение со свертыванием (схлопыванием) исходных данных и формирование результата обучения на основе лучшего результата из комитета полученных нейросетей.
Чтобы больше не возвращаться к скриптингу, сформируем общий командный скрипт, формирующий наборы данных для обучения и дающий нам результирующий ответ нейрона на произвольное значение параметров [SERVER_SEED_HASH], [NONCE]. Скрипт getanswer.sh:
#!/bin/bash
#getanswer.sh
echo «1 512 2» > ./tdata.txt
node getbitmap.js $1 >> ./tdata.txt
echo «1 0» >> ./tdata.txt
./genldata.sh 50000 $2
./trainann.sh
./sfann —do-running —test ./tdata.txt —load-ann ./maxtrain.ann
Оценка результатов обучения нейронной сети
В общем командном скрипте нет результатов применения нейрона к произвольному тестовому набору данных, на анализе которых мы остановимся более детально, чтобы оценить полученные результаты. Также для оценки результатов нам понадобится детальный вывод процесса обучения комитета нейросетей из скрипта trainann.sh, приведенного выше. Последовательно вызовем обе операции чтобы оценить полученный результат обучения:
>./sfann -v —do-cross-validation —train ./ldata.txt —num-hidden 2 —cv-num-folds 4 —cv-num-dev 2 —save-max-dev-run ./maxtrain.ann —max-epoch 10000
...
>./sfann —do-running —test ./tdata.txt —load-ann ./maxtest.ann
> Loading ./maxtrain.an ... Ok !
> Classification — 49.03%
Чтобы осознать, что мы получили в результате, возвращаемся к разделу «Немного теории» данной статьи, а именно к тезису:
...
2. Обученный нейрон или нейронная сеть на неполном множестве значений однозначно классифицирует значение на обучаемом множестве{1..N} и в соответствии с нормальным законом распределения случайных величин, производит с бóльшей вероятностью классификацию ошибки (F2(N+1) < 0,5) на неизвестном множестве {N+1..∞} при последующих значениях N → ∞ полного множества обучения.
...
Результат классификации ошибки обучения:
100% — 49.03 = 50.97%
Как и предполагалось, мы получили подтверждение нашей теории о классификации ошибки на открытом обучающем множестве с вероятностью > 0,5, или получили вероятность результата классификации ошибки более 50%!
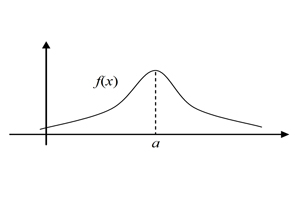
В исходном виде распределение значений больших данных неизвестного происхождения (в данном случае хэш-коды исходных данных) выглядят как и положено нормальному распределению, и результат соревнований стремится к 0,5 при N → ∞, как и показано на рис. 2.
Обучив нейрон на неполных данных и классифицировав часть его подмножества X → ∞, мы искусственно сформировали преимущество в сторону классификации ошибки Re:
Re=1-(0,5-∆)
Где Re при N → ∞ заранее известно будет иметь значение более 0,5. Количество классифицированных нейроном значений на ограниченной выборке-подмножестве {1..X} полного множества {1..N} всегда будет положительно:
{1..N}>{1..X}
Таким образом, применяя способ управления ошибкой обучения нейросетей, вероятность которой более 0,5, на неполных открытых множествах или ограниченных множествах Big Data, мы получаем статистическое преимущество > 0,5.
- Это означает, что мы в общем состязании классификации бесконечных результатов никогда не проиграем и на больших или бесконечных выборках у нас сильный союзник — нормальный закон распределения.
- Используя свойства классификации нейронными сетями и управляя ошибкой обучения на неполных выборках, при N → ∞ мы в любом случае и всегда выйдем победителем, поскольку наше статистическое преимущество > 0,5 и обеспечивает нам его тот же закон нормального распределения бесконечных случайных величин.
Именно по этой причине после обучения нейрона на подмножествах больших и бесконечных данных в прямом применении вы не увидите на тестовых выборках результат классификации данных > 0,5, и это очень важный прикладной вывод, степень важности которого сложно переоценить, но мы попробуем и туда немного заглянуть.
Выводы о полученных результатах
Классическое использование нейросетей в повседневной практике пока что рассматривается большинством в контексте классификации полных наборов данных, объемы которых ничтожно малы по сравнению с объемами Big Data и бесконечных наборов данных Infinity Data. Алгоритмы хэширования и шифрования генерируют множества значений, являющихся частным случаем Big Data/Infinity Data.
Возвращаясь к правилам нашего соревнования, наш нейрон на выходе имеет всего два значения, одно из которых будет неправильным, другое — правильным. Чтобы получить статистическое преимущество > 0,5, нам необходимо всего лишь изменить формулировку своей исходной задачи, чтобы победить в общем соревновании и в состязании не руководствоваться результатом прямого применения нейросети, а руководствоваться ошибкой обучения нейросети.
Как видно из вышеуказанного примера, условия задачи, которую мы пытались решить, были самыми жестокими и детально приведены в «Условиях проведения испытаний» настоящей статьи.
Многоуровневая защита несколькими неприступными технологиями шифрования, «соль» в исходных данных, арифметические операции и устранение части данных сдались перед нашим способом подхода к решению задачи, и мы все-таки получили вероятность положительного исхода соревнования более 0,5 как на ограниченных выборках Big Data, так и на неизвестных бесконечных наборах Infinity Data. В этом нам помогли свойства нейронных сетей в установлении корелляций/классификации не только данных, но и ошибки, и как ни странно — сам закон нормального распределения бесконечных случайных величин.
В заключение выводов просьба также обратить внимание на внешний вид графика нормального распределения именно на его пиковую часть (рис. 2). Произведя классификацию ограниченного подмножества, мы искусственно сместили вероятность общего исхода всех событий, но насколько велико наше преимущество?!
На разных типах и объемах данных данная величина естественно будет разной, однако степень влияния можно оценить уже сейчас. Например произведя нейронную классификацию 1 млн. значений подмножества N из 2512 значений, мы получили статистическое преимущество почти в 1% (для данных условий значение получено эмпирическим способом, и оно находится в диапазоне
Игры в сторону, теперь серьезно об осознанных последствиях управления ошибкой обучения нейросетей
Исследователи нейронных сетей до сих пор изучают их прямые свойства и даже после получения результатов рассматривают их как черный ящик. В настоящем исследовании мы заглянули в нейросети совсем с другой стороны, а именно со стороны управления ошибкой обучения на больших и бесконечных данных. Что нам это дало, кроме преимущества в том соревновании?
- Чтобы получить преимущество в соревновании на больших и бесконечных данных, мы изменили подход к оценке результатов обучения нейросетей и перешли к оценке результатов ошибки их обучения.
- Мы еще раз подтвердили, что нейросети являются пока самым эффективным и универсальным инструментом в классификации и анализе любых данных, как ограниченных, так и больших или бесконечных.
- Как это ни печально осознавать, мы на случайных, больших и бесконечных данных получили статистическое преимущество > 0,5, или более 50%, что означает, что мы определили путь компрометирования сколь угодно сложных технологий шифрования, имеющихся в настоящий момент на вооружении.
Преимущества полученных результатов мы обсудили, давайте затронем и негативные стороны полученных результатов.
Перейдя к способу изменения постановки задачи и анализу ошибки обучения нейросетей на больших и бесконечных данных, мы на практике нашли путь, которым можем сформировать условия решения задач в Big Data и Infinity Data, в том числе и решения задач в огромных степенях криптостойкости любых алгоритмов, не используя огромные ресурсы хранения данных обучения и большие вычислительные ресурсы.
Например, используя комитеты нейросетей с управлением ошибкой обучения и формулируя им задачи:
- установки алфавита исходных строк;
- определения длин хэшируемых значений;
- предопределения любых других вторичных операций, базирующихся на сколь угодно сложных технологиях шифрования (а на данной основе построено практически все цифровое развитие общества в настоящий момент).
Опасность неконтролируемых путей развития нейронных сетей и искусственного интеллекта сложно переоценить, и управление ошибкой обучения — всего лишь один из выявленных эффективных способов получения результатов. Здесь я могу только полностью согласиться с выводами покойного Стивена Хокинга и Илона Маска: опасность неконтролируемого роста и распространения нейронных технологий и искусственного интеллекта — реальна. В настоящих исследованиях мы просто продемонстрировали эти выводы на реальном частном случае.
Заключение
Данные материалы представлены в полном объеме, включая все необходимые инструкции, описания и программное обеспечение, доступное для свободной загрузки всем желающим. Материалы уже около полугода проходят проверку в среде специалистов по информационным технологиям, искусственному интеллекту, криптографии и прикладной математике. Пока ни одного опровержения представленным тут выводам я не получил. Материалы представляются всем желающим как отправная точка для развития исследовательских направлений полученных результатов проведенных исследований с категорическим условием: не использовать данные материалы для вредоносных целей.
Автор статьи — советник генерального директора CorpSoft24 по техническим вопросам.