От игры “жизнь” до игры КТОР
Владимир Бронников
Шахматы - это своего рода дрозофила
искусственного интелекта.
Д. Мичи, Р. Джонстон
История
В этой статье мы продолжаем тему, которая была сформулирована нами в статье “Жизнь и компьютер” (см. PC Week/RE, № 26, с. 32), но не в части обсуждения фундаментальных проблем компьютерной индустрии, а в части прикладного значения теории КА (клеточных автоматов). Мы расскажем о новых интеллектуальных играх, способных, по нашему мнению, потеснить “старые” игры, так как они больше соответствуют сегодняшним представлениям о том, что такое интеллект (искусственный и естественный). Как известно, достойные игры изобретают раз в 1000 лет (шахматы, шашки, го, рендзю), популярность их остается неизменной на протяжении тысячелетий и распределяется по странам мира в зависимости от культурных и исторических традиций этих стран. Го - самая популярная игра в Японии (по статистике в нее регулярно играют 20 млн. человек!). Шахматы - игра более известная в Европе и Америке (хотя в Америке все-таки большей популярностью пользуется реверси). Во что будут играть в России после шахмат (это ведь привнесенная игра, хотя и безусловно великая), пока не знаем, может быть, XX век породил в нашей стране новую игру и она распространится по всему миру?
Лет 10 назад автор статьи мирно писал свою докторскую диссертацию по теории клеточных автоматов и почитывал лекции по моделированию биологических систем студентам университета. Для того чтобы как-то объяснять студентам-биологам такие сложные понятия, как универсальная имитационная модель биосистемы (и ее реализация на компьютере), пришлось придумать массу моделей частных биологических систем и процессов, основанных на КА (клеточных автоматах). В результате одного компьютерного эксперимента мне пришла в голову мысль разработать оптимальные правила для интеллектуальной игры, которая в последствии получила название КТОР (клеточный тор). Два года ушло на составление правил и разработку теории игры, попутно она была выпущена тиражом 100 тыс. экз. (благо появились кооперативы) и даже широко освещалась в прессе (в том числе в известной колонке журнала “Наука и жизнь”). Конечно же, диссертация оказалась заброшена (да и другие интересы появились), но приятное чувство первооткрывателя было вознаграждено, и игра стала жить независимо от меня.
Эта публикация - первая (не считая электронного варианта моей книги на www.lanck.ru) после многих лет, прошедших с изобретения игры и ее бурного развития в течение 2 - 3 лет (проводились даже чемпионаты Ленинграда и существовал клуб любителей игры, а некоторые мои студенты уже защитили свои докторские диссертации все по той же теме КА!).
“Жизнь” Конвея и КТОР Бронникова
Игра “Жизнь” Дж. Конвея, основанная на идее Дж. фон Неймана (1971), оказалась настолько привлекательной, что практически редкая книга по математической биологии не упоминала ее - Гроснер, Тернер (1983), Эйген, Винклер (1979), Фомин, Беркенблитт (1976). И что не менее удивительно, эта игра часто приводится в руководствах по программированию в качестве изящной и простой модели естественных процессов в искусственно созданных клетках из единиц и нулей (из битов) - Уэзерелл (1982), Касаткин (1980), Эткинс (1987). Конечно же, к биологическим процессам игра “Жизнь” имеет косвенное отношение, однако ее популярность объясняется простотой правил и сложностью получающихся пространственных конфигураций клеток. Это пример процесса, который на элементарном уровне организации примитивен, но, будучи включен в систему кооперативного поведения тысячи клеток, приводит к сложным следствиям, непредсказуемым, если исходить из свойств отдельных элементов. Более глубокие аналогии с биологическими процессами возможны на основе теории обобщенных клеточных автоматов (В. Бронников, 1988), для которых игра Конвея является просто частным случаем. Здесь мы будем рассматривать игру “Жизнь” только как прототип игры КТОР и поэтому отметим некоторые общие черты.
В игре “Жизнь” все события происходят на плоской решетке, часто с замкнутыми на тор краями, и то же самое можно сказать об игре КТОР. Клетка в игре “Жизнь” может находиться в двух состояниях: живая и мертвая. В игре КТОР это свойство остается, но появляются живые клетки двух типов: свои и противника. На этом сходство кончаются и начинаются различия.
Во-первых, сложность поведения отдельной фишки (или клетки) в игре КТОР намного выше, чем в игре “Жизнь”, она как бы уже напоминает реальную живую систему (клетку, животное и т. п.) и может не только рождаться и умирать, но и мигрировать, “летать”, внезапно исчезать и появляться в другой части поля. Можно сказать, что фишка в КТОРе обладает большим числом степеней свободы и в этом она больше похожа на клеточный автомат, который имеет 29 состояний - автомат Дж. фон Неймана (1971).
Во-вторых, существенное отличие заключается в том, что процессы в игре “Жизнь” происходят параллельно по всей плоскости, что означает возможность одновременного изменения всех клеток поля при выполнении условия, определенного локальной функцией переходов. Если размер поля 30х30 или 100х100 клеток, то человек уже не в состоянии осуществить это преобразование, ведь наш мозг не приспособлен к выполнению большого числа логических операций (попробуйте сосчитать за 1 секунду, сколько точек в кадре телевизионного изображения, а машине эта операция покажется самой простой). Крайний случай игры мог бы выглядеть, как процесс, в котором за один такт времени изменения происходят в отдельной клетке поля, тогда этот процесс окажется достаточно простым, чтобы человек смог его произвести мысленно. Действительно, два различных по степени параллельности процесса приводят к двум различным механизмам мышления - параллельной и последовательной обработке. Поэтому в игре КТОР мы сознательно выбрали некоторый оптимум параллельности, еще доступный для человека по числу локальных операций, которые можно реализовать за один такт времени.
Еще одна особенность связана с начальными условиями игры. Для сложных процессов, происходящих в биологических системах, начальные условия системы не задают однозначно их поведения во времени. В искусственных же системах (таких, как игра “Жизнь”) наоборот - из одного и того же начального состояния (т. е. из одной и той же конфигурации) получается одна и та же финальная структура. Процесс в этом случае является сложным, но детерминированным. В игре КТОР имеется несколько механизмов, из-за которых поведение игрока и соответственно позиции на доске нельзя считать детерминированными - это, конечно же, действия противника. Однако механизм “комбинационного взрыва”, характерный для шахмат, когда на каждый полуход число возможных ответов возрастает как степенная функция, вполне сохраняется и в игре КТОР.
Поведение биологической системы, как мы уже отмечали, можно описать как клеточный автомат, но этому будет посвящена отдельная статья. Заметим только, что при создании алгоритмов игры для компьютера нас ожидают не меньшие трудности, чем создателей шахматных программ, поскольку, по нашему мнению, игра КТОР не менее (если не более) сложна для компьютерного моделирования, чем шахматы или го. Тем более, что, в отличие от этих игр, в КТОРе пока нет таких богатых теорий и практических достижений и, главное, игрового опыта. Но те, кто рискнет последовать за нами, получат огромное удовлетворение от чувства первооткрывателей. Первое описание алгоритма для игры в шахматы дал К. Шеннон (1948), и с тех пор число конструктивных идей не очень возросло (см. в этой связи предисловие В. А. Криницкого к книге М. М. Ботвинника). Даже успехи программы IBM в последнем матче с Каспаровым в июне 1997 г. изменяют ситуацию несущественно, поскольку затраченные ресурсы и время не стоили того, чтобы доказать очевидное - компьютер в состоянии считать быстрее, чем человек! Нам бы хотелось, чтобы после нашего описания игры КТОР ее не постигла бы та же участь, что и шахматы. И для этого есть все основания. Шахматы подчиняются статичным правилам, а КТОР - это динамическая система с бесконечным множеством правил и неограниченным числом стратегий.
Тем более что игра в игру - это не только забава, но, по нашему глубокому убеждению, и способ овладеть новым видением виртуального мира алгоритмов, подготовить свое мышление к восприятию естественной параллельности процессов, которые, хочется нам или нет, происходят в природе независимо от того, знаем ли мы единственное описывающее их дифференциальное уравнение (и существует ли таковое вообще!).
Новая интеллектуальная игра КТОР
Познание атома - это детская игра
по сравнению с познанием детской игры.
Альберт Эйнштейн
Поле для игры КТОР
Одной из основных особенностей игры КТОР является необычная организация поля. Возьмем лист бумаги и соединим два противоположных края листа - получим цилиндр. Затем соединим концы цилиндра и получим трехмерную фигуру - тор (или бублик). Отличительная особенность этой фигуры в том, что, двигаясь по ее поверхности, мы не сможем обнаружить края плоскости. В то время как во всех логических играх (го, реверси, рендзю, шахматы и шашки) поле ограничено краем доски, что, кстати, сильно отражается на стратегиях этих игр (вспомните борьбу за центр в шахматном дебюте!). Фигуры типа тора уже использовались при разработке новых игр, например в цилиндрических шахматах и играх в числа на торе (см. Е. Я. Гик, 1985, А. Б. Бойко, 1987), а также в качестве основы для моделирования экологической системы (см. А. К. Дъюдни, 1985). Конечно, играть на таком поле, как тор, не очень удобно, однако оно вполне приемлемо для компьютера.

Владимир БРОННИКОВ -директор
по маркетингу компании “ЛАНК”
Так как наше мышление “привыкло” к поверхностям более простым (прямоугольники, квадраты и т. п.), мы можем использовать для игры КТОР плоское поле, т. е. развертку тора (бублика). Для этого произведем операцию, обратную предыдущей: развернув бублик по линиям, по которым мы сворачивали лист бумаги, получим поле для игры.
Если оставить поле в таком виде, то игроку все время придется помнить о том, что на самом деле поле - это поверхность бублика, и играть будет сложно (особенно начинающим). Поэтому придуманы очень простые и наглядные обозначения “крайних” клеток плоского поля. Они показаны на рис. 1. Здесь внутреннее поле (ограниченное внутренним рядом цифр) - это собственно игровое поле (или, как его называют, основное поле), а крайние клетки (внешний ряд цифр) - это дополнительное поле - часть основного поля, перенесенная в соответствии с правилами развертки бублика на противоположную сторону (можно использовать и цвет для изображения типов соответствующих друг другу клеток). Эта операция развертывания бублика, конечно, более элегантна в компьютерном варианте игры, когда вместо обычной доски используется экран дисплея и машина автоматически соблюдает правило связывания противоположных краев поля. Для игры на реальной доске дополнительное поле дублирует все пограничные клетки основного поля, чтобы игроку было удобнее представлять, что у основного поля нет логической границы и оно продолжается на противоположной стороне плоского листа.
Правила игры КТОР
Для игры КТОР, так же как для игры го, можно использовать фишки двух цветов или двухсторонние фишки, как в реверси. Число фишек должно быть не меньше числа клеток поля (основного и дополнительного). Поле для игры выбирается размером от 9х9 до 19х19 клеток в зависимости от силы играющих. Мы рекомендуем играть на поле размера 15х15, именно такое поле принято в официальных соревнованиях и выпускается в виде игровых комплектов.
Партия начинается с пустого поля. Игроки по очереди делают свои ходы. Выигрывает тот, у кого окажется больше фишек на основном поле после того, как все клетки поля будут заполнены. Существует правило первого хода. Это правило гласит, что тот, кто ходит первым, ставит только одну фишку, а второй играющий ставит уже две фишки.
Для того чтобы рассмотреть правила ходов, давайте сначала порассуждаем, какие действия возможны для отдельных фишек на плоскости и как еще можно “усложнить” поле для игры, чтобы она стала более интересной. При этом мы будем считать, что сложность игры возрастает, если возрастает сложность поведения отдельного элемента (фишки) или у фишки появляются новые возможности, которых не было раньше. Подобное мы наблюдаем в природе: сложность поведения человека намного превосходит сложность поведения пчелы за счет сложности самой организации человека как биологического вида. Отсюда точно предсказать репертуар всех человеческих реакций сложнее, чем поведение пчелы.
И хотя наша игра - лишь очень приблизительная копия клеточной организации, тем не менее основные атрибуты особи (или клетки) как элемента популяции мы в нее ввели.
Так что же может отдельная фишка? Прежде всего, она должна как-то появляться на поле, по аналогии с жизнью - рождаться. В игре участвуют два партнера, они и будут “родителями” наших фишек, т. е. каждый игрок может выставлять свои фишки на поле. Итак, первая возможность хода или отдельная операция для данного хода - постановка фишки на поле.
Таблица уровней сложности игры КТОР
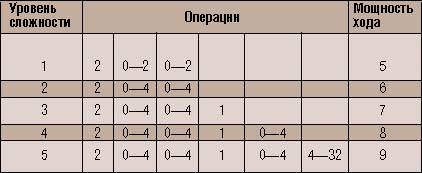
Обозначения операций: 1 -постановка фишки; 2 -перемещение фишки;
3 - замена фишки; 4 - десант; 5 - миграция группы фишек; 6 - операция "черная дыра".
Суммарная мощность, указанная в столбце "мощность хода", равняется
сумме мощностей всех операций данного уровня сложности без учета
операции "черная дыра". Если мощности зафиксированы для каждой
операции в отдельности (например 2, 0, 2, 1, 2, 0), то вариант называется
жестким, в противном случае - мягким.
Понятно, что ход может состоять из нескольких отдельных операций, но мы пока использовали только одну. Для удобства игры введем понятие - “мощность операции”. Мощность соответствует числу поставленных фишек за один ход одним игроком или тому, сколько раз данная операция применяется за один ход. Так можно говорить о мощности 2 для операции “постановка”, если правилами предусмотрено, что за один ход противники могут поставить на поле не более двух своих фишек. Вспомните, и у человека редко рождается одновременно пять или шесть детей, чаще один, иногда - двое. А что может произойти с фишкой, оказавшейся на поле? Тут ее подстерегают явные и скрытые опасности - фишки противника и черные дыры. Сейчас мы определим, в чем эти опасности заключаются.
Мы введем механизм уничтожения фишек противника. Итак, вторая возможная операция в течение одного хода противников - замена фишки противника на свою фишку (или переворот фишки на поле, как в реверси). Условием замены фишки противника является наличие как минимум (можно и больше) пяти своих фишек вокруг атакуемой фишки противника. Мы не будем здесь обосновывать это условие, укажем только, что оно выбрано не случайно, а вытекает и из геометрии двухмерной решетки, на которой идет игра, и из тонкого соотношения между устойчивостью и неустойчивостью возникающих на поле позиций (для подробного анализа этого свойства автору понадобился компьютер! И два года работы). Для этой операции, так же как для операции “постановка фишки”, можно ввести понятие мощности - сколько фишек можно заменить за один ход.
Даже при таких простых правилах игра приобретает новые свойства по сравнению с известными играми. Можно уже попробовать поиграть и убедиться в этом. Чего же еще не хватает в действиях фишек, чтобы игра стала еще динамичней? (Кстати, если ограничиться изложенными правилами, то игра обладает всеми свойствами реверси, не считая особенностей игрового поля).
Уже упоминавшаяся игра го, которой увлечены сегодня миллионы людей, ставит своей целью захват максимального пространства доски. Создание связных цепочек на доске из своих фишек и организация групп возможны только за счет постановки фишек и взятия в плен групп фишек противника. В шашках и шахматах основу составляет не операция постановки (разве что в начале партии надо научиться правильно расставить свои фигуры на доске), а операция перемещения фишек (фигур) по полю. А что, если совместить возможности постановки фишек во время партии и перемещение во время игры своих фишек?
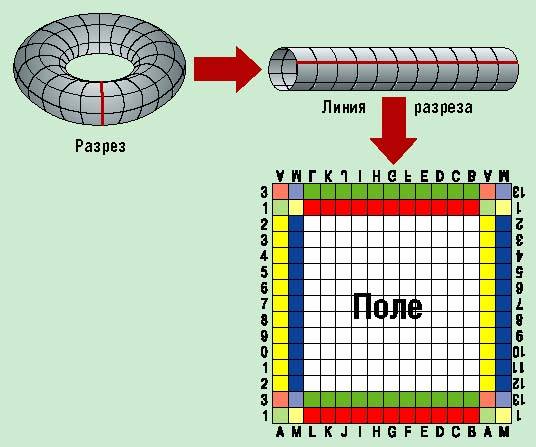
Создание поля для игры в КТОР
Для этого введем новую операцию - перемещение фишки. Самый простой вариант перемещения - на одну клетку, например по вертикали или по горизонтали. Эта операция преображает игру (можно сказать, до неузнаваемости) - появляются более богатые возможности маневра (в буквальном и переносном смысле). Итак, подытожим наши изыскания. За один ход противники могут совершить следующие действия, которые мы назвали операциями: а) поставить заданное число фишек на свободные клетки поля; б) переместить фишку на заданное число позиций или несколько фишек в сумме на это же число позиций; в) заменить заданное число фишек, если выполнено условие замены.
Теперь остается решить вопрос с мощностью отдельных операций, т. е. сколько раз за один ход можно применять данную операцию? Вариантов было перепробовано множество, но на практике наиболее интересными оказались несколько. Один из самых популярных вариантов, это когда две фишки ставятся, две могут быть перемещены и две - заменены за один ход. Таким образом, мы с вами узнали об учебном варианте игры КТОР. Большую динамичность дает вариант, который был применен на первенстве Ленинграда 1988 г. среди школьников: а) число фишек для постановки - 2; б) мощность операций “замена” и “перемещение” в сумме равна 4; в) все операции (или их часть) выполняются в течение одного хода в любом порядке.
Кстати, даже такой простой вариант крайне непросто реализовать в виде компьютерной игровой программы. Для более сложных вариантов игры мы не беремся предсказать возможность создания программы, играющей в силу мастера (по крайне мере, сделать ее будет гораздо сложнее, чем для шахмат или го).
Уровни сложности КТОР
(дополнительные операции в игре: миграция, десант, черная дыра)
Думаю, уже ясно, что чем больше операций можно использовать за ход и чем выше их мощность, (т. е. чем больше “свобода выбора” во время отдельного хода), тем сложнее становится игра. Как найти тот оптимум, при котором правила все еще обозримы и доступны игроку, но уже настолько богаты по своим возможностям, что делают игру практически бесконечной? Нам кажется, что такой оптимум найден в правилах игры КТОР, попробуем в этом убедить читателя.
При разыгрывании партий в учебном варианте часто возникает ситуация, когда игрок сосредоточил свои фишки в одной части поля, а события стали развиваться в другой его части, и игрок, естественно, хочет перебросить свои силы. Если ставить (как это разрешено в учебном варианте) по две фишки за ход в зоне “прорыва”, то потребуется несколько ходов, чтобы укрепить свою позицию. Поэтому в игру дополнительно вводятся новые операции, которых, кстати сказать, нет в других играх такого типа.
Операция “десант” позволяет перебросить свои ресурсы из одной части поля в другую (на любое расстояние). Для этого с поля снимаются две любые фишки, а вместо них выставляется одна фишка, но на любую свободную клетку поля. Это позволяет перегруппировать свои силы, и хотя при этом происходит потеря количества, зато возрастает качество!
Вторая операция служит также цели переброски ресурсов. Она называется “миграция”. В процессе перемещается не отдельная фишка, как это было в операции перемещения, а группы из двух, трех и четырех фишек, так как это показано на рис. 2.
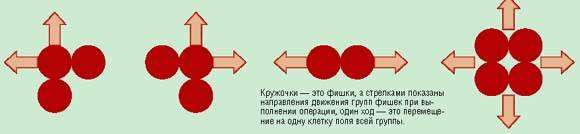
И та и другая операции могут выполняться многократно за один ход, т. е. обладать соответствующей мощностью. Попробуйте теперь сыграть партию, и вы убедитесь, что игра стала намного интереснее. У нее появилось новое свойство. Логический анализ, который спасал вас в более простых вариантах игры, уже не помогает, поскольку на поле за один ход может происходить достаточно много непредсказуемых изменений. Здесь начинает работать в полную силу ваше образное мышление и интуиция!
Нам осталось рассмотреть самую экзотическую операцию, которая пока еще не применяется в официальных соревнованиях, но является настолько необычной, что мы приводим ее описание для тех, кто хочет достигнуть совершенства в игре КТОР. Эта необычная операция называется “черная дыра”.
Представим себе, что у нас в руках спица и мы протыкаем тор (т. е. бублик) насквозь. Точка входа в поверхность называется истоком черной дыры, а точка выхода - стоком. Эта операция переворачивает наши представления о связанном игровом поле, так как нарушается топология плоской развертки! Но она приводит к тому, что игрок теперь в состоянии контролировать удаленные от его позиции клетки игрового поля и, более того, разрушать устойчивые конфигурации фишек противника, которые другим путем (устойчивые позиции) не берутся.
Перед началом партии противники выбирают (общие для обоих игроков) пары координат на игровом поле, с тем чтобы в ходе игры их можно было использовать для создания черных дыр. Создание черной дыры происходит следующим образом. Одна из помеченных в паре клеток окружается пятью своими фишками, это будет означать, что вы организовали исток черной дыры, и сразу же в точке стока появляется ваша фишка (вы, независимо от того, стояла ли там фишка противника, ставите дополнительно свою фишку в клетку стока). Эта фишка (стоящая в стоке) неуязвима для противника, однако она не может перемещаться или мигрировать из места стока и не может быть использована в операции “десант”. Ее можно использовать только для операции “замена фишки”. Причем фишка-сток исчезает, когда мы освобождаем исток.
Число черных дыр на поле должно выбираться исходя из того, чтобы на игровом поле одни зоны не становились предпочтительнее других. Лучше всего для этой цели использовать случайный процесс или компьютер. Число черных дыр можно варьировать, и это зависит от силы играющих. Для более точной рекомендации требуется специальное исследование на компьютере.
Рассмотрим теперь таблицу уровней сложности игры КТОР. В ней представлено пять уровней сложности, причем мощности отдельных операций указаны в отдельном диапазоне. Это означает, что операция может принимать значение мощности в одном ходе от минимальной, указанной в таблице (например, 0), до максимальной (например, 2, смотри строку “уровень сложности 1”).
Компьютерный вариант игры КТОР
Компьютеры применяются как для разыгрывания партий между двумя партнерами, так и для игры с машинной программой. Они широко используются для контроля ходов, записи партий и демонстрации в шашках, шахматах, реверси. Для игры КТОР также очень удобно использовать компьютер, особенно это относится к верхним уровням сложности, когда число и мощность операций возрастают. Для пятого уровня сложности можно не только генерировать координаты черных дыр, но и заставить машину быть третьим партнером в игре, перемещая или генерируя черные дыры по ходу партии. Еще более интересным может оказаться вариант, когда черная дыра “поглощает” часть пространства в истоке и возвращает его в области стока. Механизмом вовлечения фишек противника в собственные фишки и появлением вероятностного правила постановки фишек на поле можно также усложнить игру, придав ей необычайный азарт и динамичность. Здесь может работать принцип - чем больше я “съедаю” фишек противника, тем ниже вероятность того, что при постановке своей фишки она действительно окажется своей! Возрастает риск хода. Компьютер можно использовать и для контроля за временем игры.
Необходимо сказать о программах, играющих в КТОР. Нам неизвестны сегодня программы, играющие на уровне сложности выше первого. А на первом уровне сложности машина проигрывает новичку уже после нескольких партий, правда, если не ведется контроль времени. Мы надеемся, что написание играющей программы может стать не только увлекательным занятием, но и послужить более эффективному освоению возможностей компьютера. Тем более что программа существенно усложняется, переходя с уровня на уровень, впрочем, как и мыслительные способности человека.
Мы описали новую игру КТОР, которая обладает свойствами, не присущими таким интеллектуальным играм, как го, реверси, рендзю и др. Будущее ее зависит от вас, от того, насколько понравится вам красота ее комбинационных возможностей, сколь интересными будут партии. Для тех, кто не пожалеет времени на освоение ее самых сложных вариантов, откроется увлекательнейший мир, в котором царят интуиция, воображение и логическое мышление.
Заключение
Игра КТОР, рассмотренная в этой статье, подтверждает, что свойствами КА не исчерпывается все многообразие алгоритмов для компьютера, а множество интуитивно понятных моделей (применяемых в социологии, химии, биологии, физике) для изучения “поведения” сложных систем, для которых не существует математического описания, говорит о том, что потенциальные возможности этой теории еще далеко не исчерпаны.
Игра КТОР способствует:
- тестированию (и тренингу) возможностей левого и правого полушарий головного мозга, поскольку в правила игры заложены регулируемые механизмы управления логическим и образным мышлением человека;
- развитию интеллектуальных способностей (зрительного восприятия и памяти);
- развитию конструкторских способностей и пространственного мышления;
- развитию воображения в варианте “невидимых” фишек противника;
- и, наконец, обучению принципам алгоритмизации и моделирования реальных систем на примере решения задач на “естественном” языке описания поведения физических и биологических систем.
Владимир Бронников - директор по маркетингу компании “ЛАНК”. С ним можно связаться по телефонам: (812) 110-6464, 325-6666 и по адресу: bva@lanck.ru. На сервере www.lanck.ru в разделе “домашние страницы” опубликована книга автора “Искусственные ограничения естественного интеллекта”, где более подробно изложены все аспекты теории КА и их применение.